Jak měřit rovinnost - technický článek
Existuje řada způsobů měření rovinnosti povrchu. Nejběžnější metodou v odvětví rovinného lapování je použití monochromatické sodíkové světelné jednotky a optické roviny. Tímto způsobem lze získat mimořádně přesná měření, která jsou přesnější než u většiny souřadnicových měřicích strojů, a to ekonomickým způsobem.
Co jsou to světelné pásy?
Světelné pásy objevil Isaac Newton, který je poprvé studoval v roce 1717. Jedná se o interferenční obrazec, který vzniká odrazem světla mezi dvěma povrchy.
Při použití monochromatického zdroje světla je možné tento jev využít k výpočtu rovinnosti součásti, ale povrch součásti musí být odrazivý, aby se světelné pásy objevily. Světelné pásy se skládají ze světlého a tmavého okraje. Jejich kombinace odpovídá vlnové délce monochromatického světla, která je v případě sodíkového zdroje rovna 589 nm. Při kontrole plochosti dílů se počítají pouze tmavé pruhy, takže vzhledem k tomu, že se jedná o polovinu celkového třásně, každý tmavý pruh se rovná 294 nm nebo 0,00029 mm.
Diamantové lapování je ideální pro vytváření reflexních povrchů, jejichž rovinnost lze touto metodou měřit přímo po lapování.
Kalkulačka rovinnosti
Typické vzory světelných pásů, které vykazují přesnost plochosti
| Geometrie povrchu | 1 světelný pás 0.00029mm | 2 světelný pás 0.00058mm | 3 světelný pás 0.00087mm | 9 světelný pás 0.00261mm | |
|---|---|---|---|---|---|
Konvexní nebo konkávníPovrch rovnoběžný s plochouSymetrický vzor |  |  | |||
KonvexníWith concave surface band will curve in opposite directionNesymetrický vzor |  | 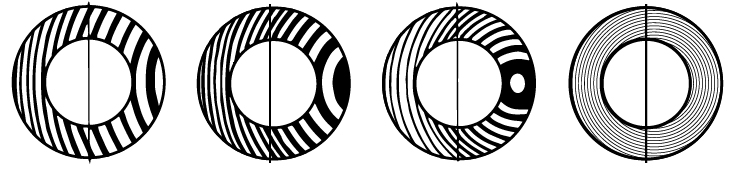 | |||
válcovýKonvexní nebo konkávníSymetrický vzor |  |  | |||
Ve tvaru sedlaSymetrický vzor | 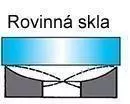 | 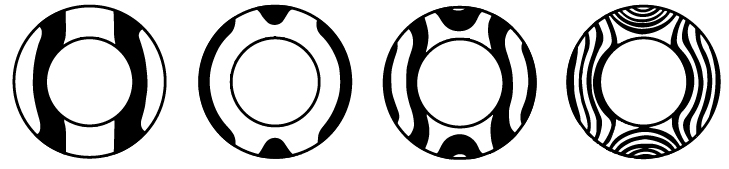 | |||
Jak číst světelné pásy pomocí optické roviny
Nejprve očistěte povrch součásti a optické plošiny pomocí kapesníku na čočky nebo měkkého hadříku, který nepouští vlákna. Obě plochy musí být naprosto čisté. Opatrně položte optickou plochu na součástku. Neposouvejte ji napříč. Jakmile se optická ploška a součástka přiblíží k sobě, objeví se na ploše čáry. Manipulujte s ní tak, abyste získali čárový vzor, jak je znázorněno na obrázku. Tyto čáry jsou interferenční třásně nebo pásy a ukazují, o kolik se povrch součástky zvedl nebo snížil vzhledem k optické ploše.
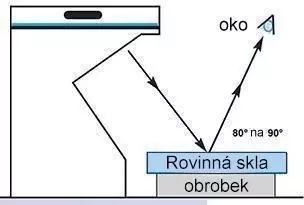
Čtení světelného pásu Ukazuje dokonalou rovinnost
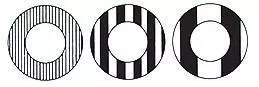
Rovinnost lapovací desky
Konvexní
Vzor prstenu se pohybuje směrem k tlaku prstů. Pokud je obrobek konvexní, je lapovací deska konkávní.
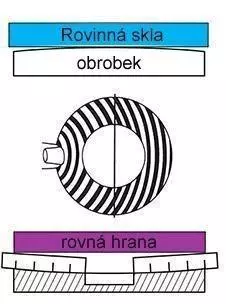
Konkávní lapovací deska
Pro nápravu tohoto stavu je třeba kontrolní kroužky přesunout na vnější stranu desky.konkávní
Vzor prstenu se od tlaku prstů vzdaluje. Pokud je obrobek konkávní, je lapovací deska konvexní.

Lapovací deska konvexní
Pro nápravu tohoto stavu je třeba kontrolní kroužky posunout na vnitřní stranu desky.Rovné rovnoběžné pásy, nikoli šířka světelného pásu, udávají rovinnost.
Graf povrchové úpravy
Povrchy se vyrábějí různými procesy odstraňování materiálu. Výslednou geometrii lze nejlépe rozdělit na tři složky - drsnost, zvlnění a tvar.
Základní parametry

Parametry - jsou znázorněny různé parametry Ra a Rt. Je vidět, že středová čára je ta čára, která rozděluje plochy tak, že: A1 + A3 + ............ A7 = A2 + A4 + ............ A8 Dvě nejběžnější měření kvality povrchu jsou Ra a Rt Jsou popsána následovně:
Ra je všeobecně uznávaným nejpoužívanějším mezinárodním parametrem drsnosti. Je to aritmetický průměr odchylek profilu drsnosti od střední čáry.
Rt je maximální výška profilu od vrcholu k údolí na měřené délce. Měření se obvykle udává v mikronech. 1 mikron = přibližně 40 mikroinchů
Příklady Ra a Rt
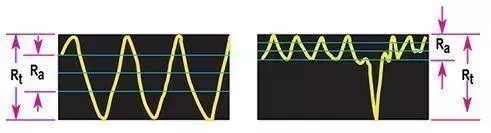
Typická prohlášení o povrchové úpravě nebo struktuře na výkresu:

Symbol A Jak zadat maximální hodnotu drsnosti v mikronech Ra.
Symbol B Jak zadat maximální a minimální hodnoty drsnosti.
Symbol C Jak zadat maximální drsnost a dokončovací proces.
Kemet převodní tabulky
| Převod imperiální do metrické soustavy | ||||
|---|---|---|---|---|
| Milimetry (mm) | Mikrony (μm) | Angstrémy (Å) | ||
| 1 INCH (1.00”) | = | 25.4 | 25,400 | 254,000,000. |
| 1 TIS. (0.001”) | = | 0.0254 | 25.4 | 254,000 |
| 1 MIKROINCH (μin) | = | 0.0000254 | 0.0254 | 254 |
| Převod metrická do imperiální | ||||
| Palce | Tisícinky | Mikropalce | ||
| 1 MILIMETR (mm) | = | 0.039 37 | 39.37 | 39,370 |
| 1 MIKRON (μm) | = | 0.000 039 37 | 0.039 37 | 39.37 |
| 1 ANGSTROM (Å) | = | 0.000 000 003 937 | 0.000 003 937 | 0.003 937 |
